Guia 1-Transformación Lineal

Posted by : lilivar lunes, 16 de marzo de 2020

Transformaciòn Lineal

GUIA DE TRABAJO - SEMANA UNO

ALGEBRA LINEAL 10ª JORNADA MAÑANA

Tema: Transformación Geométrica. Aplicación del producto entre matrices

Objetivos:

Identificar las matrices en el campo geométrico
Aplicar el producto entre matrices para resolver problemas de transformación geométrica
Representar los elementos de las matrices como punto de coordenadas en el plano cartesiano

Marco Teórico

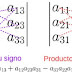
El álgebra lineal es importante para abarcar asignaturas de algunas de las carreras universitarias, es por esta razón que se involucra el álgebra lineal en la media para fortalecer procesos cognitivos, procedimentales y resolución de problemas en los estudiantes a partir conceptos y operaciones adquiridas implementando Aplicaciones álgebra lineal en este caso producto entre matrices en el campo Geometrico

Ingresa al blog allí encontraras todo lo relacionado con las explicaciones del tema para que realices tus actividades

ü https://matematicasabordo.blogspot.com/

ü Clic en 10ª

ü Revisa los recursos digitales dejados allí

ü Elabora la actividad y envía antes de la fecha

Actividad (en hojas milimetradas dibuja, opera, dibuja y escanea. Convierte a pdf y envía)

Ubica cada uno de los siguientes pares ordenados en el plano cartesiano.
Realiza el producto entre matrices según la transformación geométrica matricial y nuevamente grafica en la hoja milimetrada
Las hojas deben estar debidamente marcadas con nombres apellidos y fecha, el titulo correspondiente a la trasformación indicada y con sus respectivos colores y uso de regla para elaborarlo

1. TRASLACION: Dada la figura formada a partir de los puntos: A (2,6); B (4,2); C (6,6); D (4,4), Obtenga su traslación por medio del método de la multiplicación, basado en los siguientes valores: T_x=-4, Tx=-1.

2. TRASLACIONES SUCESIVAS: Dada la figura formada a partir de los puntos: A (2,2); B (4,2); C (3,5); D (2,4), Aplique traslaciones sucesivas Vt₁= (-2,2), Vt₂= (5,0)

3. REFLEXION: Dada la figura formada a partir de los puntos: A (1,1); B (2,1); C (3,3); D (2,2), E (1,3), Determine su posición después de aplicar una reflexión en torno al eje “y”. Luego realice a esta última figura una reflexión en torno al eje “y aplique una reflexión en torno al origen.

4. ESCALAMIENTO Dada la figura formada a partir de los puntos: A (2,6); B (4,2); C (6,3); D (4,6), aplique un escalamiento S_X= (2, ½) y un vector de traslación V_T= (5,6)

5. ROTACION: Dada la figura formada a partir de los puntos: A (5,4); B (8,6); C (11,4); D (11,6), Aplicar una reflexión en torno al eje “x” y partiendo de las dos figuras anteriores aplica una rotación de 90ª